Résumé
     On étudie, dans cet article, différentes solutions de pompes à chaleur pour une maison typique de la région parisienne. Le cas d’un échangeur utilisant un forage vertical dans le sol est étudié et comparé aux solutions plus simples de PAC air-air, avec ou sans complément consommant avec un rendement au plus égal à 1 de la chaleur primaire ou de l’électricité. Il est montré que la solution géothermique n’apporte au mieux qu’un faible gain énergétique et qu’elle est donc très loin d’être économiquement rentable à cause de l’important investissement supplémentaire qu’elle nécessite. 

La pompe à chaleur
     La pompe à chaleur est une machine thermodynamique qui permet de transférer de la chaleur d’une source froide à une source (plus) chaude. 
     Pour chauffer une maison, on puisera donc de la chaleur à l’extérieur pour maintenir la température de la maison à 20°C. 
     Le coefficient de performance (COP) d’une pompe à chaleur est le rapport entre l’énergie fournie (pour le chauffage) et l’énergie consommée. Pour un convecteur électrique, ce rapport vaut 1. Le COP augmente quand la température de la source froide se rapproche de celle du point chaud (voir annexe A). Il n’est en principe jamais inférieur à 1.

Pompes air-air 
     Le coefficient de performance d’une pompe à chaleur moderne air-air évolue, d’après le constructeur, d’environ 2,5 (pour une température extérieure de -10°C) à 3,5 (pour une température extérieure de 15°C).
     D’après des bilans de consommation réalisés dans une maison particulière, ce même coefficient de performance – intégrant la consommation du ventilateur de l’unité intérieure et les phases de dégivrage pendant laquelle la pompe s’inverse – varie entre 1,8 et 2,3 pour les mêmes températures. 

Pompe air-eau
     Comme la performance d’une PAC diminue lorsque l’écart entre la température de la source chaude et celle de la source froide augmente, les systèmes utilisant l’eau pour chauffer la maison doivent être dimensionnés de sorte que la température de l’eau soit aussi basse que possible, ce qui implique des débits plus importants pour fournir la même quantité de chaleur nécessaire au chauffage.
     Un système de chauffage par le sol est donc plus indiqué qu’un système de radiateurs. Un cas particulier est celui des PAC air-eau utilisées pour préchauffer l’eau des systèmes à chauffage central classiques (déjà existants). Pour une température d’eau chaude de 45°C, le COP donné par le constructeur varie de 2.54 pour une température extérieure de -7 à 3.78 pour une température extérieure de 20. On peut donc supposer (espérer) que la qualité de l’échange dans l’unité intérieure contribue à améliorer le COP par rapport aux systèmes air-air. 

Pompe géothermique 
     Il n’y a pas de raison majeure pour estimer que le COP d’une pompe géothermique est très différent de celui des autres pompes à chaleur. Si toutefois on considère que l’échangeur de l’unité extérieure fonctionne avec un fluide caloporteur (qui va chercher la chaleur dans le sol) on peut, de manière optimiste, considérer que le problème du givrage est évité. 
     On retiendra donc une valeur du COP plus élevée que lorsque l’air est utilisé comme source froide. On verra par la suite que, dans certaines configurations, la source froide pourrait atteindre des températures très basses. C’est la raison pour laquelle le COP est prolongé vers les basses températures, la valeur 1 étant atteinte lorsque la température extérieure vaut -20°, valeur voisine de la température d’évaporation du fluide frigorifique. 
     La température moyenne annuelle en région parisienne étant d’environ 12°C et en considérant un gradient géothermique optimiste de 30°C par km, on peut estimer à 15°C la température-profondeur. Elle est de 22°C à 500 m de profondeur près de Bar-le-Duc). Elle sera plus froide vers le haut et plus chaude vers le bas, mais on négligera cette variation relativement faible dans le cas d’un échangeur vertical. 
     Le liquide utilisé dans l’échangeur du forage n’est pas du fréon (car cela représenterait un trop grand volume, vu le coût de ce fluide) mais de l’eau avec antigel qui ne gèle pas au dessus de -20°C. 
     En considérant que ce système n’est pas affecté par le dégivrage, et en négligeant les inévitables pertes dans un échangeur eau glycolée – fréon, on prendra comme COP de la PAC la valeur nominale de la pompe air-air donnée par le constructeur. Bien sûr, ce coefficient chute considérablement lorsque la température descend et, en supposant que le liquide ne gèle jamais, on supposera simplement que le COP vaut 1 en dessous de -20°C, ce qui signifie qu’on ne puise alors plus de chaleur dans le sol. 
     On notera que cette estimation est optimiste car les constructeurs ne donnent pas de valeur pour le COP en dessous de -10°C. La température de liquéfaction du fréon se situe vers -25°C à la pression atmosphérique. 
     Les différents COP évoqués sont représentés sur la Figure 1, fonction de la température extérieure, pour une température intérieure de 20°C:

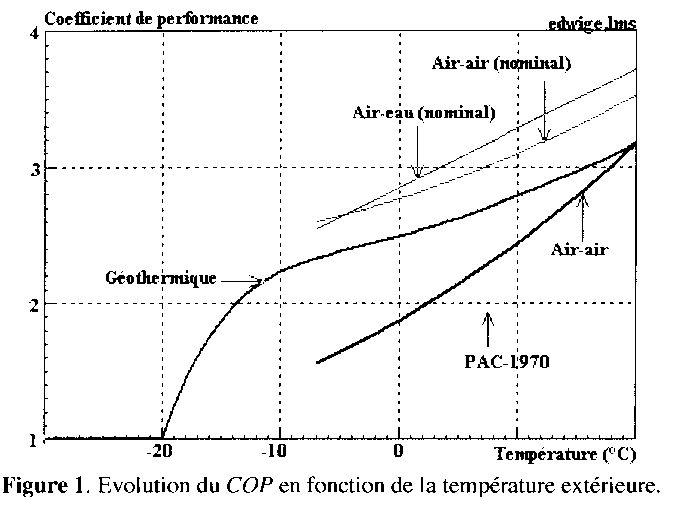
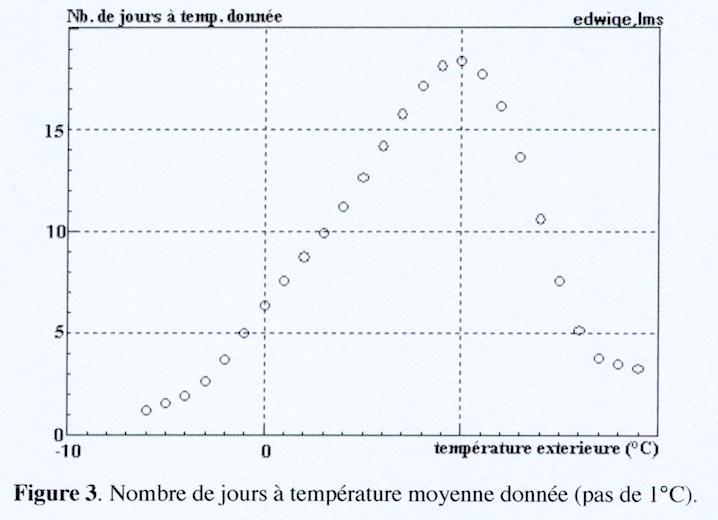
Figure 1
Evolution du COP en fonction de la température extérieure

Figure 2
Courbe des fréquences cumulées des températures moyennes journalière pour la période de chauffage allant du 1er octobre au 31 mai

     L’information qui nous intéresse est contenue dans la «courbe des fréquences cumulées des températures moyennes journalières». On représente en ordonnée, le nombre de jours pour lesquels la température est supérieure ou égale à une valeur donnée, en abscisse. 
     On s’aperçoit en l’observant (Figure 2) que la température moyenne journalière n’est inférieure à 0° qu’une vingtaine de jours par an.

     En utilisant ces données et le COP de la pompe on peut facilement comparer l’énergie nécessaire au chauffage à celle fournie par la pompe pour une température donnée compte tenu du nombre de jours pendant lesquels la température a eu cette valeur (Figure 3). On vérifie (Figure 4) que le gain apporté par la PAC ne devient significatif que pour les températures positives. Deux effets pour l’expliquer se conjuguent: un meilleur COP et davantage de jours à température positive.

Figure 4
Energie consommée à température moyenne donnée

     (un point correspond à la quantité annuelle d’énergie associée au nombre de jours pour lesquels la température moyenne a eu la valeur en abscisse -avec un pas de 1°C). La courbe «besoin» correspond à l’énergie fournie par la pompe ou à la consommation d’un chauffage par convecteurs. 
     On peut donc se demander s’il n’est pas économiquement plus intéressant de diminuer la puissance thermodynamique installée et de la compléter par des résistances, de coût en investissement inférieur, quand le COP est trop bas.

Figure 5
Energie consommée à température donnée

     (Comme pour la Figure 4, un point correspond à la quantité annuelle d’énergie associée au nombre de jours pour lesquels la température moyenne a eu la valeur en abscisse. On a ici relié les points par des segments de droite).
     On observe que l’économie (surface entre la courbe du «besoin» et l’énergie fournie) ne diminue pas très sensiblement en diminuant la puissance thermodynamique installée. 
     Pour un besoin total annuel de 20.000 kWh, l’énergie nécessaire est respectivement de 10.700, 10.300 et 9.200 kWh pour les PAC de puissance 6, 3 et 2 kW. L’écart de gain entre la puissance maximale et la puissance de 2kW (au demeurant suffisante pour assurer au besoin la climatisation l’été) n’est que de 1.500 KWh par an (soit une valeur de l’ordre de 150 € à comparer au surcoût d’une PAC de 6 kW par rapport à une de 2 kW). 

B. Source froide enterrée (réseau de canalisations à faible profondeur) 
     Il est généralement admis que le sol ne gèle pas en dessous d’une certaine profondeur, de l’ordre du mètre. On peut donc penser qu’un échangeur utilisant un fluide caloporteur dans un réseau légèrement enterré va améliorer l’efficacité de la PAC, par rapport à un système air-air, en procurant une source de chaleur à température plus élevée que la température de l’air extérieur. 
     La réalité est un peu plus complexe. En effet, on sait que les variations de température entre le jour et la nuit se font ressentir jusqu’à une profondeur de l’ordre de 1 m. La température du fluide dans le sol sera donc, en moyenne, la même que la température extérieure et il y a donc peu à gagner, sauf peut-être du côté du COP s’il les problèmes de givrage sont éliminés. 
     De plus, le sol est un mauvais conducteur. C’est d’ailleurs pour cette raison qu’on stockait autrefois la glace d’hiver dans la terre pour la conserver pour une utilisation l’été (Bien sûr, l’importante chaleur de fusion de la glace (équivalente à celle nécessaire pour une élévation de température de la même masse d’eau de 80°C) contribuait sensiblement à la réussite de l’opération). On peut donc craindre que le volume de sol refroidi par la PAC devienne rapidement une barrière isolante n’améliorant pas le fonctionnement du système. C’est ce que confirme une étude expérimentale [1] résumée sur la Figure 6.

     D. Système (dit) géothermique
     Dans le cas de la véritable géothermie, c’est-à-dire de la disposition d’une source quasi illimitée à température élevée, son utilisation comme source chaude paraît intéressante si sa température est supérieure à celle de l’air ambiant. 
     Reste le problème de la mauvaise conductivité du sol qui nécessite une évaluation plus approfondie. On montrera en effet que l’extraction d’un flux de chaleur du sol entraîne une baisse de température au niveau de l’échangeur et il faut en tenir compte pour connaître l’efficacité de la pompe, puis l’économie annuelle moyenne. 
     On s’intéresse au cas d’un forage vertical d’une centaine de mètres de profondeur. On considère, comme indiqué plus haut, que 15°C est une température optimiste du sol à 100 m de profondeur. 
     Deux options technologiques sont possibles:
     - Le forage lui-même est isolé et on place l’échangeur au fond du trou. On suppose qu’il a alors une forme sphérique de rayon donné et on modélise le problème par celui d’un trou sphérique situé dans un massif rocheux initialement à 15°C. 
     - L’autre option consiste à utiliser le forage sur toute sa hauteur ou en tout cas en dessous d’une profondeur d’une dizaine de mètres où la température du sol n’est pas affectée par les variations climatiques annuelles. On modélise alors le problème par celui d’un cylindre dont les faces horizontales sont isolées situé dans un massif infini initialement à une température de 15°C (ce qui est légèrement optimiste). 
     La solution de ces deux problèmes est donnée en annexe B. A titre indicatif, on y évalue également comme cas particulier le cas simple (et idéal) où la source de chaleur à 15° est illimitée. 
     On en déduit que le trou sphérique est totalement irréaliste et qu’en revanche, le trou cylindrique mérite d’être étudié. On se limitera au trou de 40 cm de diamètre, ce qui est plutôt optimiste car nécessitant l’extraction d’un gros volume de déblais. On présente sur la Figure 7, analogue à la figure 5, les efficacités comparées des différents systèmes. 
     Pour l’ensemble des calculs présentés en annexe, les caractéristiques du sol utilisées sont les suivantes. [http://archi.climatic.free.fr/calculs/calculs.html] La thermique volumique des roches est de l’ordre de 550 Wh/m³/°C. En prenant la valeur optimiste de 0.004 m²/h (plus le sol est conducteur, plus l’échange de chaleur sera facile) on en déduit une valeur de la conductivité de 2.16 W/m²/°C. Il est indiqué que le sol saturé a une meilleure conductivité que le sol sec, ce qui explique sans doute cet écart. Si toutefois le sol est saturé mais que l’eau circule très peu – ce qui est le cas général-, on ne peut attendre d’amélioration car la conductivité de l’eau est plus faible que celle de la roche. On prendra pour la conductivité, une valeur de 3 W/m²/°C qu’on doit donc considérer comme optimiste.

Figure 7
Comparaison des efficacités énergétiques³

Conductivité K: 3 W/m/°C  (0.007 cal/s/m/°C)
Capacité calorifique volumique Cv: 550 Wh/m³
Capacité calorifique massique  Cv: 240 Wh/t (0.2 cal/g)
Diffusivité thermique (associée à K) k: 1.6 10-6 m²/s (0.0055 m²/h - 48 m²/an)

(3- un point correspond à la quantité annuelle d’énergie associée au nombre de jours pour lesquels la température moyenne a eu la valeur en abscisses)
     Il apparaît que la solution géothermique apporte un léger gain par rapport à la PAC air-air, gain presque aussi important que dans le cas optimal de la source infinie à température constante. 
     Toutefois, rapporté à la totalité des besoins, ce supplément de gain est peu significatif. En effet, l’économie annuelle serait de 64%. Par rapport aux 53% obtenus avec une PAC air-air, le gain est modeste (de l’ordre de 2.300 kWh) alors que l’installation est bien plus onéreuse et susceptible de se dégrader avec le temps sans possibilité aisée de réparer (gel, corrosion, fuites..). Le choix économique se pose dans les mêmes termes que celui de la puissance thermodynamique d’un simple système air-air (Figure5)

Discussion
      Rappelons d’abord que le choix d’un forage thermiquement isolé, avec échangeur au fond, est aberrant. Seul le cas d’un échangeur vertical tout le long du forage mérite d’être considéré.
     On peut se demander si l’utilisation du forage dit «géothermique» deviendrait intéressante dans une région plus froide. 
     Ce n’est pas a priori le cas car la température moyenne du sol est égale à celle de la surface augmentée du même gradient géothermique. On ne pourrait gagner un peu qu’à démontrer que le COP de la PAC géothermique est moins affecté par la chute de température que celui de la PAC air- air. 
     Dans le cas du cylindre, il n’en est rien car le résultat est peu affecté par le diamètre du cylindre et le coût d’un forage plus profond est bien supérieur à celui de plusieurs forages, à hauteur totale équivalente. Cela ne compenserait pas le gain dû à l’augmentation de la température moyenne. 
     Dans le cas de la sphère, c’est pire car on n’atteindrait pas des dimensions raisonnables. Il faudrait en effet augmenter le rayon de la sphère au moins comme celui de la puissance extraite, ce qui conduirait à une énorme augmentation des déblais à extraire. 

Conclusion
     La faible conductivité du sol compense l’intérêt de son utilisation comme source de chaleur et le cas d’une source idéale lui-même ne présente qu’un faible gain de consommation à mettre en regard de l’important investissement correspondant et de la fiabilité à long terme du système. 
     Dans ce cas particulier, la solution de l’échangeur en fond d’un puits isolé, échangeur dont la surface sera nécessairement modeste, est en tout cas à bannir. Seul un échangeur vertical le long du puits ne donne pas un résultat plus mauvais que celui d’une simple pompe air-air. 
      Le meilleur choix économique pour une pompe à chaleur est donc le système le plus simple de la pompe air-air qui présente en outre l’avantage de permettre facilement la climatisation l’été. 

     On constate que ce COP dépend très fortement du rayon de la sphère creusée au fond du puits. 
     Le système est moins efficace que la pompe à chaleur air-air si le rayon du trou est inférieur à 3 m.
     Pour s’approcher de la solution idéale – source infinie à 15°C -, il faut considérer un trou de 20 m de rayon, totalement irréaliste. Un trou de (seulement!) 3 m de rayon correspond à un volume de 110 m³ et une masse de 260 tonnes...
     On peut ensuite utiliser ce résultat - par un calcul identique à ceux réalisés avec des températures de source froide connues -, en tenant compte des besoins annuels. 

     On cherche la solution pour différents diamètres de trou et une température initiale du sol de 15°C. Contrairement au cas de la sphère, la température ne se stabilise jamais et continue à baisser tant qu’on extrait de la puissance calorifique. Ceci n’empêche pas d’évaluer de manière raisonnable le fonctionnement du système car la température diminue de manière logarithmique et donc est quasiment stabilisée au bout d’un temps raisonnable. 
     Une solution plus exacte du problème nécessiterait des calculs compliqués qui ne sont pas justifiés ici. Il faudrait en effet résoudre le même problème avec un champ de température initial non homogène. Dans ces conditions, il semble raisonnable d’étudier le fonctionnement du système sur une période assez longue d’une vingtaine de jours et pour une température moyenne de –2°C, ce qu’on peut estimer d’après la figure 2. 
 Pour les valeurs qui nous intéressent, on représente sur la figure B3, l’évolution de l’écart de température en fonction du temps pour une puissance extraite de 2,5 kW. En effet, pour une température moyenne de –2°C, la puissance nécessaire au chauffage de l’habitation est de 7 kW et on table sur un coefficient de performance de 2,7. 
     On observe que la variation de température dépend assez peu du rayon du cylindre. De toute façon, elle est suffisamment faible pour que son effet sur le coefficient de performance de la pompe ne soit pas significatif. 

Figure B3
Évolution de l’écart de température au bord du trou sur 20 jours. (pour une puissance extraite de 2,5 kW)

     Il est difficile d’avancer une hypothèse simple sur le retour à l’état initial de la température du massif. Comme pour la sphère, on peut supposer que le temps de retour à l’équilibre est du même ordre de grandeur que le temps nécessaire pour atteindre un déséquilibre donné. Mais ce temps caractéristique est ici beaucoup plus long. On peut toutefois calculer que l’écart de température doublerait (seulement) de valeur entre 20 jours et six mois de fonctionnement.
     Au regard de la figure B3, on considèrera donc que, pour les paramètres de cette étude, le cas du cylindre vertical de 40 cm de diamètre et 80 m de haut peut être estimé en considérant qu’il se comporte à peu près comme une sphère de 40 m de diamètre.